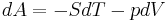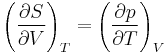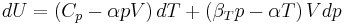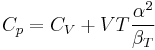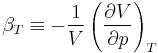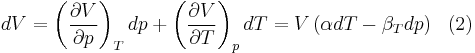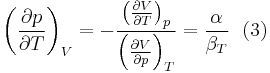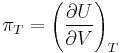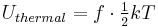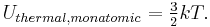Internal energy
| Thermodynamics | |||||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||||
In thermodynamics, the internal energy of a thermodynamic system, or a body with well-defined boundaries, denoted by U, or sometimes E, is the total of the kinetic energy due to the motion of particles (translational, rotational, vibrational) and the potential energy associated with the vibrational and electric energy of atoms within molecules or crystals. It includes the energy in all of the chemical bonds, and the energy of the free, conduction electrons in metals.
One can also calculate the internal energy of electromagnetic or black body radiation. It is a state function of a system, and is an extensive quantity. The SI unit of energy is the joule although other historical, conventional units are still in use, such as the (small and large) calorie for heat.
One can have a corresponding intensive thermodynamic property called specific internal energy, commonly symbolized by the lower-case letter u, which is internal energy per mass of the substance in question. As such, the SI unit of specific internal energy would be the J/kg. If intensive internal energy is expressed on an amount of substance basis, then it could be referred to as molar internal energy and the unit would be the J/mol.
Contents |
Overview
Internal energy does not include the translational or rotational kinetic energy of a body as a whole. It excludes any potential energy a body may have because of its location in external gravitational or electrostatic field, although the potential energy it has in a field due to an induced electric or magnetic dipole moment does count, as does the energy of deformation of solids (stress-strain). The principle of equipartition of energy in classical statistical mechanics states that each molecular quadratic degree of freedom receives 1/2 kT of energy, [1] a result which had to be modified when quantum mechanics explained certain anomalies, such as discrepancies in the observed specific heats of crystals when the expected thermal energy per degree of freedom is less than the energy necessary to move that degree of freedom up one quantum energy level.
For monoatomic helium and other noble gases, the internal energy consists only of the translational kinetic energy of the individual atoms. Monoatomic particles, of course, do not (sensibly) rotate or vibrate, and are not electronically excited to higher energies except at very high temperatures.
From the standpoint of statistical mechanics, the internal energy is equal to the ensemble average of the total energy of the system. It is also called Intrinsic energy.
Composition
Internal energy is the sum of all forms of energy of a system. It is related to the molecular structure and the degree of molecular activity and may be viewed as the sum of kinetic and potential energies of the molecules; it is composed of the following types of energies:
| Composition Components of internal energy contained within a system. |
Thermal energy | The sum of all energies that give rise to the temperature of a system | |
| Chemical energy | Energy due to the chemical composition and configuration of a system, some of it may be available as a driving force for chemical reactions. | ||
| Nuclear energy | The large amount of energy associated with interactions within the nuclei of atoms. | ||
| Interactions Processes that can change the internal energy of a system by transferring energy across the system boundary. |
Heat transfer | Energy transfer driven by a temperature difference. | |
| Work | Energy transfer driven by changes in macroscopic physical properties of a system. | ||
| Mass transfer | Energy transferred by mass flowing across a system boundary. | ||
The first law of thermodynamics
The internal energy is essentially defined by the first law of thermodynamics which states that energy is conserved:
where
- ΔU is the change in internal energy of a system during a process.
- Q is heat added to a system (measured in joules in SI); that is, a positive value for Q represents heat flow into a system while a negative value denotes heat flow out of a system.
- W is the mechanical work done on a system (measured in joules in SI)
- W' is energy added by all other processes
The first law may be stated equivalently in infinitesimal terms as:
where the terms now represent infinitesimal amounts of the respective quantities. The d before the internal energy function indicates that it is an exact differential. In other words it is a state function or a value which can be assigned to the system. On the other hand, the δ's before the other terms indicate that they describe increments of energy which are not state functions but rather they are processes by which the internal energy is changed. (See the discussion in the first law article.)
From a microscopic point of view, the internal energy may be found in many different forms. For a gas it may consist almost entirely of the kinetic energy of the gas molecules. It may also consist of the potential energy of these molecules in a gravitational, electric, or magnetic field. For any material, solid, liquid or gaseous, it may also consist of the potential energy of attraction or repulsion between the individual molecules of the material.
Expressions for the internal energy
The internal energy may be expressed in terms of other thermodynamic parameters. Each term is composed of an intensive variable (a generalized force) and its conjugate infinitesimal extensive variable (a generalized displacement).
For example, for a non-viscous fluid, the mechanical work done on the system may be related to the pressure p and volume V. The pressure is the intensive generalized force, while the volume is the extensive generalized displacement:
Taking the default direction of work, 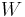 , to be from the working fluid to the surroundings,
, to be from the working fluid to the surroundings,
Taking the default direction of heat transfer, 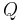 , to be into the working fluid and assuming a reversible process, we have
, to be into the working fluid and assuming a reversible process, we have
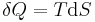 .
.
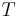 is temperature
is temperature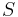 is entropy
is entropy
The above two equations in the first law of thermodynamics imply for a closed system:
If we also include the dependence on the numbers of particles in the system, the internal energy function may be written as 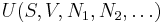 where the
where the 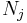 are the numbers of particles of type j in the system. U is an extensive function, so when considered as a function of the extensive variables variables S, V, and the particle numbers
are the numbers of particles of type j in the system. U is an extensive function, so when considered as a function of the extensive variables variables S, V, and the particle numbers 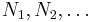 , we have:
, we have:
From Euler's homogeneous function theorem we may now write the internal energy as:
where the 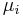 are the chemical potentials for the particles of type i in the system. These are defined as:
are the chemical potentials for the particles of type i in the system. These are defined as:
For an elastic substance the mechanical term must be replaced by the more general expression involving the stress 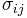 and strain
and strain 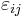 . The infinitesimal statement is:
. The infinitesimal statement is:
where Einstein notation has been used for the tensors, in which there is a summation over all repeated indices in the product term. The Euler theorem yields for the internal energy:[3]
For a linearly elastic material, the stress can be related to the strain by:
The path integral Monte Carlo method is a numerical approach for determining the values of internal energy, based on quantum dynamical principles.
Changes in internal energy
The expressions given above for the internal energy involves the entropy. In practice one often wants to know the change in internal energy of a substance as a function of the change in temperature and volume, or as a function of the change in temperature and pressure.
Changes due to temperature and volume
The expression relating changes in internal energy to changes in temperature and volume is
This is useful if the equation of state is known. In case of an ideal gas, 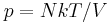 which implies that
which implies that 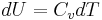 , i.e. the internal energy of an ideal gas can be written as a function that depends only on the temperature.
, i.e. the internal energy of an ideal gas can be written as a function that depends only on the temperature.
To express dU in terms of dT and dV, we substitute
in the fundamental thermodynamic relation
This gives:
The term 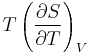 is the heat capacity at constant volume
is the heat capacity at constant volume 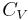 .
.
The partial derivative of S with respect to V can be evaluated if the equation of state is known. From the fundamental thermodynamic relation, it follows that the differential of the Helmholtz free energy A is given by:
The symmetry of second derivatives of A with respect to T and V yields the Maxwell relation:
This gives the expression above.
Changes due to temperature and pressure
When dealing with fluids or solids, an expression in terms of the temperature and pressure is usually more useful:
where we have used that the heat capacity at constant pressure is related to the heat capacity at constant volume according to:
The partial derivative of the pressure with respect to temperature at constant volume can be expressed in terms of the coefficient of thermal expansion
and the isothermal compressibility
by writing:
and equating dV to zero and solving for the ratio dp/dT. This gives:
Substituting (2) and (3) in (1) gives the above expression.
Changes due to volume at constant pressure
The internal pressure is defined as a partial derivative of internal energy with respect to volume at constant temperature:
Equipartition theorem
The equipartition theorem yields simple expressions for the thermal energy. In case of an ideal gas, the thermal energy is exactly given by the kinetic energy of the constituent particles. The internal energy per particle is equivalent to the average translational kinetic energy of each particle. Ignoring quantum effects, this is given by equipartition of energy.[4]
According to the equipartition theorem, the thermal energy of a molecule in a thermal bath is
where f is the number of degrees of freedom, T is the temperature, and k is Boltzmann's constant. For example, for a monatomic ideal gas, each particle has three degrees of freedom, and thus
When the spacing between the energy levels of a particular degree of freedom becomes of the order of k T or less, the energy in that degree of freedom becomes less than given by the equipartition theorem and it vanishes exponentially as k T becomes much less than the energy difference. The system is then frozen in the ground state.
For a gas at room temperature at normal densities, the vibrational degrees of freedom are usually frozen, while the rotational and vibrational degrees of freedom can be treated classically. Quantum effects for the translational degrees of freedom become important when the specific volume per particle is of the same order or smaller than 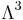 where
where 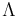 is the thermal de Broglie wavelength. In this regime quantum statistical effects become important. Depending on whether the molecules are Fermions or Bosons, the gas will become a degenerate Fermi gas or a Bose-Einstein condensate, respectively. E.g., at room temperature, the electrons in a metal form a degenerate Fermi gas, the internal energy per electron is of the order of
is the thermal de Broglie wavelength. In this regime quantum statistical effects become important. Depending on whether the molecules are Fermions or Bosons, the gas will become a degenerate Fermi gas or a Bose-Einstein condensate, respectively. E.g., at room temperature, the electrons in a metal form a degenerate Fermi gas, the internal energy per electron is of the order of  with
with 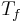 the Fermi temperature which can be of the order of 80,000 K. So, in this case, the equipartition theorem underestimates the internal energy by many orders of magnitude.
the Fermi temperature which can be of the order of 80,000 K. So, in this case, the equipartition theorem underestimates the internal energy by many orders of magnitude.
History
James Joule studied the relationship between heat, work, and temperature. He observed that if he did mechanical work on a fluid, such as water, by agitating the fluid, its temperature increased. He proposed that the mechanical work he was doing on the system was converted to "thermal energy". Specifically, he found that 4200 joules of energy were needed to raise the temperature of a kilogram of water by one degree Celsius.
Notes
- ↑ Reif, Frederick (1965). Statistical Physics. New York: McGraw-Hill Book Company. pp. 246–250.
- ↑ Cengel, Yungus, A.; Boles, Michael (2002). Thermodynamics - An Engineering Approach, 4th ed.. McGraw-Hill. pp. 17–18. ISBN 0-07-238332-1.
- ↑ Landau & Lifshitz 1986.
- ↑ Thermal energy – Hyperphysics
References
- Alberty, R. A. (2001). "Use of Legendre transforms in chemical thermodynamics" (PDF). Pure Appl. Chem. 73 (8): 1349–1380. doi:10.1351/pac200173081349. http://www.iupac.org/publications/pac/2001/pdf/7308x1349.pdf.
- Lewis, Gilbert Newton; Randall, Merle: Revised by Pitzer, Kenneth S. & Brewer, Leo (1961). Thermodynamics (2nd ed.). New York, NY USA: McGraw-Hill Book Co.. ISBN 0-07-113809-9.
- Landau, L. D.; Lifshitz, E. M. (1986) (in English). Theory of Elasticity (Course of Theoretical Physics Volume 7). (Translated from Russian by J.B. Sykes and W.H. Reid) (Third ed.). Boston, MA: Butterworth Heinemann. ISBN 0-7506-2633-X.
See also
- Calorimetry
- Enthalpy
- Gibbs free energy
- Helmholtz free energy
- Thermodynamic equations
- Thermodynamic potentials
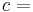
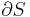
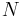
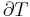
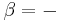
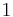
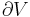
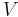
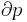
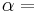
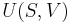


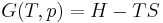
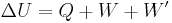
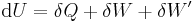
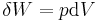 .
.
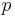 is the
is the 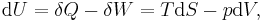
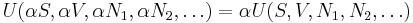

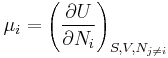
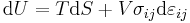
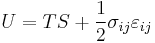
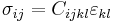
![dU =C_{V}dT +\left[T\left(\frac{\partial p}{\partial T}\right)_{V} - p\right]dV\,\,\text{ (1)}\,](/I/b09679c40217cda00140f8bd4abf17df.png)
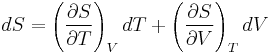

![dU = T\left(\frac{\partial S}{\partial T}\right)_{V}dT +\left[T\left(\frac{\partial S}{\partial V}\right)_{T} - p\right]dV\,](/I/9a873395d8c94f1bfd5c36a38f32808f.png)